Tutorial 6 . Contours
Tutorial 6 describes how eli application reads objects contours and how contours can be display on picture. Tutorial explains contours parameters.
Eli application uses contours parameters for objects description program. Execution of object description program founds object on cameras, pictures or videos.
Find contours, draw contours
- Load test program basic2.eli from previous tutorials.
- You should have 5 test program lines.
- Put cursor on the last line of test program by left click on line 5 (Conversion_Morfology).
- Select command Find from Contours commands group and click on Add button
- Keep cursor on inserted line (Contours_Find) and go to the Select command window.
- Select Source_picture to Picture_1 on command Contours_Find. It is input picture. It should be binary image. We create binary image on line 4 and changed it on line 5.
- Select Contours parameter to Contour_0. It is contour array where fount contours will be stored. You can select another contour array but you need to use it in the next steps.
- Keep lines 3 to line 6 in default setup. Those lines setup offset (see command documentation for better explanation of offset).
- The last line 7 is used for storing number of founds contours to some system variable.
- Click on button Change for save command changes.
- Keep Test program cursor on the last line (Contours_Find).
- Select command Draw from Contours command group and click on Add button.
- Keep cursor on inserted line (Contours_Draw) and go to the Select command window.
- Select Picture_0 on the first command parameter (Source_picture). It is original 3 channel picture. Fount contours will be draw on original picture. Do not use Picture_1. Picture_0 is single channel binary image and it is better to write colored contours and it is possible only on 3-channel picture .
- Select Contour_0 as a Contours parameter. It is contours array where fount contours is stored in previous command.
- Click on Contour color parameter. Color dialog displays. Select color which should be used for contours drawing.
- Set Tickness parameter to 2. It is contours line thickness in pixels.
- Keep line type parameter to 8. It is contour line type
- Click on button Change for save command changes.
- Change display picture on command System_Results to Picture_0 and click on button Change for save command changes.
- Run test program and source picture with drawn contours displays in Picture window.
- Save this test program as basic3.eli. We will use it in the next tutorials.
Contours parameters
Next part of this tutorial explains contours parameters. Those parameters is using during object description programs.
It is mathematical description of contours. Results of this mathematical description are using in object description programs.
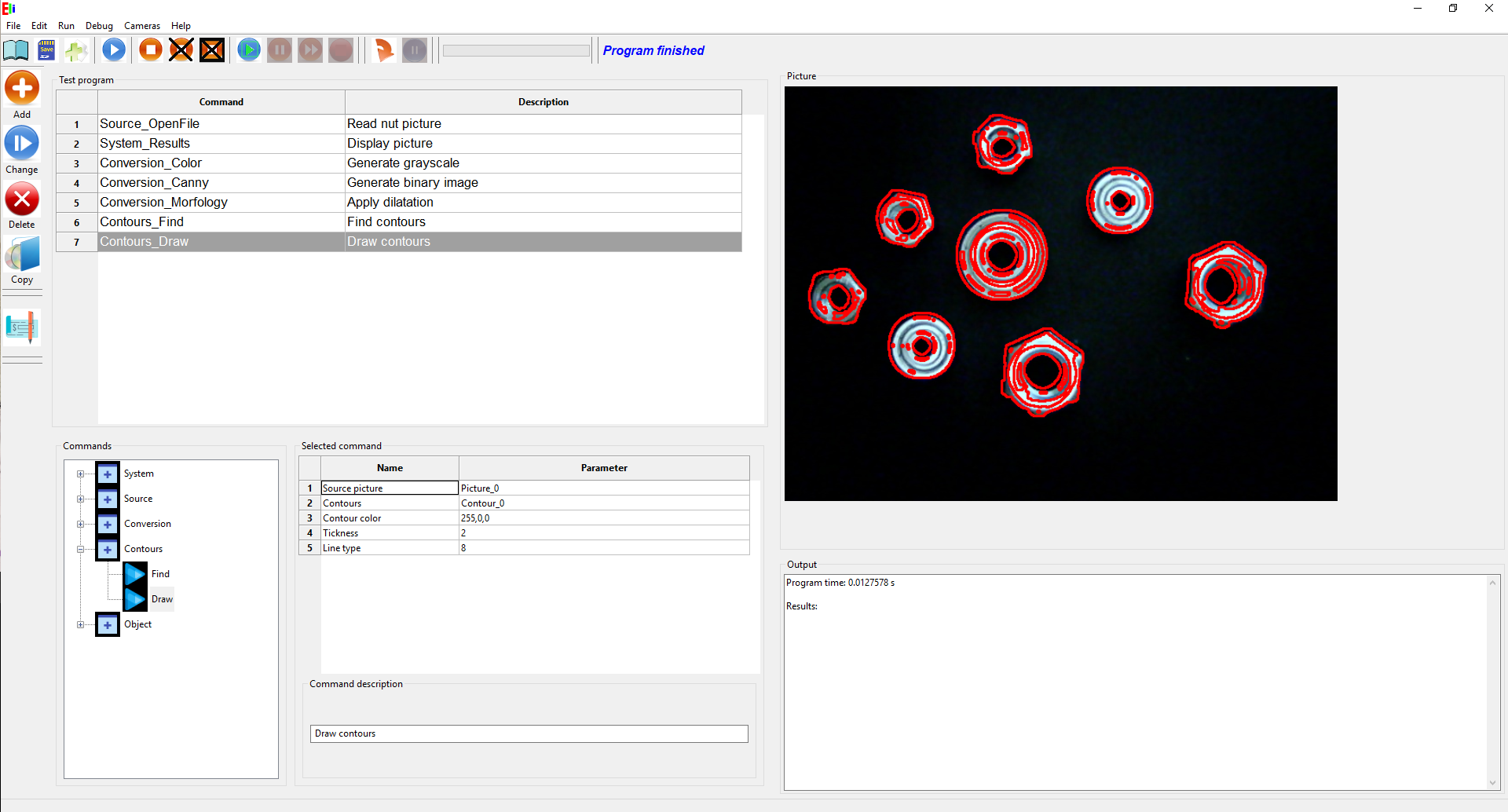
Bounding Rectangle
Bounding rectangle is rectangle around all object. Bounding rectangle has 4 parameters:
- Bounding rect X: X coordinate in left top point of rectangle
- Bounding rect Y: Y coordinate in left top point of rectangle
- Bounding rect width: Width of rectangle
- Bounding rect height: Height of rectangle
Contour area and perimeter
Contour area is number of all pixels in the object represented by contour
Perimeter is length of contour over object
Perimeter is length of contour over object

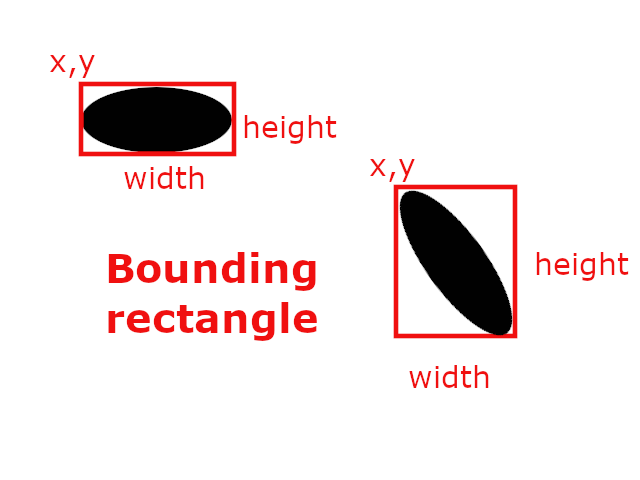
Minimal area rectangle
It is minimal rectangle over all object. Rectangle also describe rotation of object
Minimal area rectangle has 5 parameters:
- Center X: X coordinate center of rectangle
- center Y: Y coordinate center of rectangle
- Size: width: Width of rectangle
- Size:height: Height of rectangle
- Angle: Rotation angle of rectangle
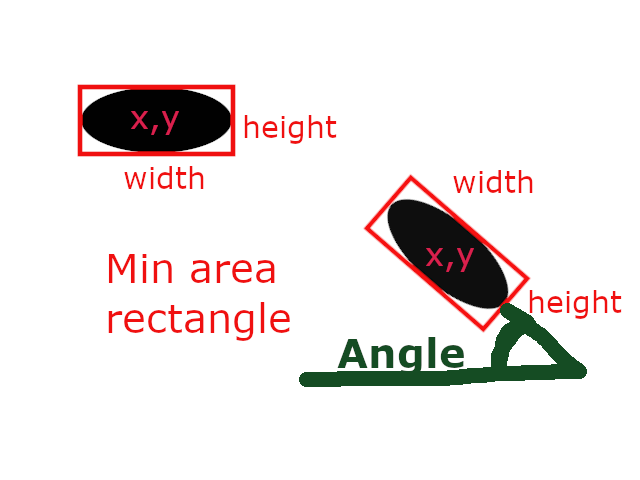
Minimal enclosing circle
It is minimal circle over all object.
Minimal enclosing circle has 5 parameters:
- Center X: X coordinate center of circle
- center Y: Y coordinate center of circle
- Radius: radius of circle

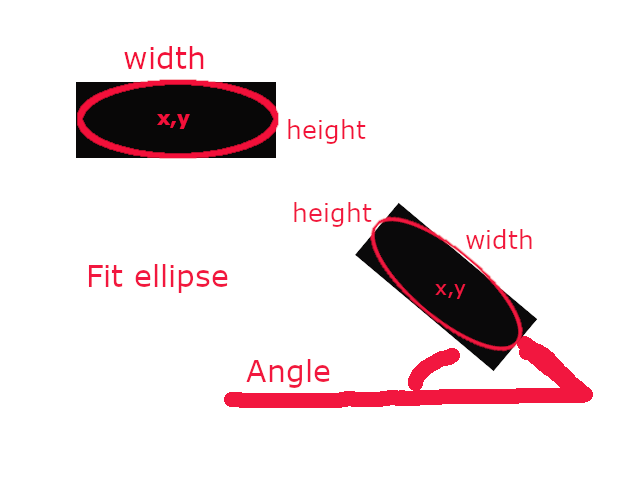
Fit ellipse
It is minimal ellipse over all object. Ellipse also describe rotation of object
fit ellipse has 5 parameters:
- Center X: X coordinate center of ellipse
- center Y: Y coordinate center of ellipse
- Size: width: Width of ellipse
- Size:height: Height of ellipse
- Angle: Rotation angle of ellipse
Moments
There are four types of moments which are calculated on contours. It is Spatial moments,Central moments, Normalized cetral moments and Hu moments
The first three moments are calculated up to the 3rd order. There are 2 picture which helps explain moments calculation. There are two different object on each picture
On the picture is same object with various position:
The first three moments are calculated up to the 3rd order. There are 2 picture which helps explain moments calculation. There are two different object on each picture
On the picture is same object with various position:
- 1: Object A in vertical position
- 2: Object A in horizontal position
- 3: Object A rotated in 45 degrees
- 4: Object A in vertical position scalled to 70% of size
- 11: Object B in vertical position
- 12: Object B in horzontal position
- 13: Object B rotated in 45 degrees
- 14: Object B in vertical position scalled to 70%of size
Object A
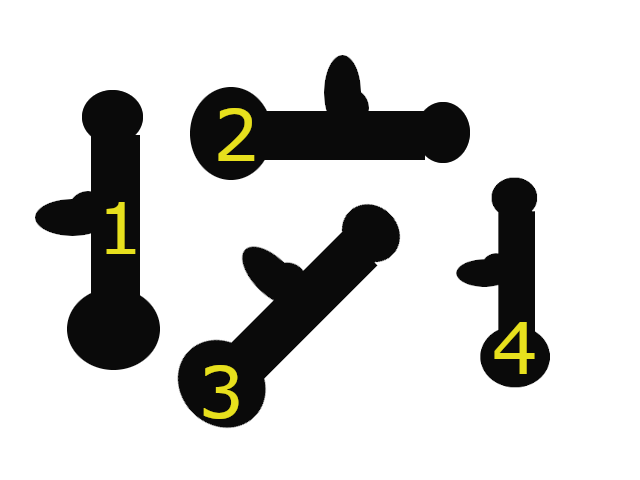
Object B
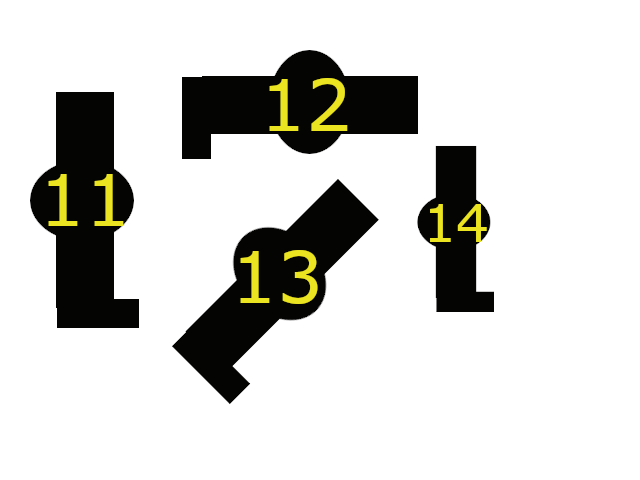
Spatial moments
Spatial moments are calculated according follow formulla:
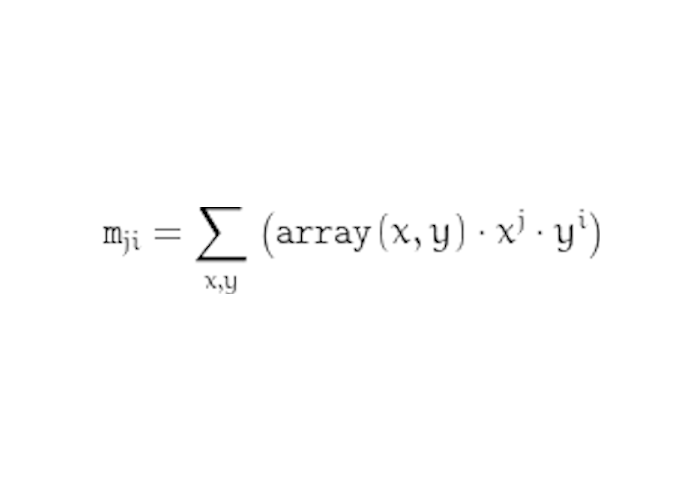
Table bellow show spatial moments on both objects on picture above
Spatial moments is raw moments. It used for calculation other types of moments
Spatial moments (0,0) is same value as contour area. If you look on the formulla it is just count of pixels
| (0 0) | (1 0) | (0 1) | (1 1) | (2 0) | (0 2) | (3 0) | (2 1) | (1 2) | (0 3) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ObjA 3 | 17737.5 | 4.99666e+06 | 5.62435e+06 | 1.53457e+09 | 1.46495e+09 | 1.84454e+09 | 4.45672e+11 | 4.3586e+11 | 4.88249e+11 | 6.23745e+11 | |
| ObjA 4 | 9929.5 | 5.07865e+06 | 2.87129e+06 | 1.46919e+09 | 2.60054e+09 | 8.64829e+08 | 1.33311e+12 | 7.52635e+11 | 4.42781e+11 | 2.69793e+11 | |
| ObjA 1 | 17759.5 | 1.93094e+06 | 4.24407e+06 | 4.63406e+08 | 2.19388e+08 | 1.12349e+09 | 2.57921e+10 | 5.29516e+10 | 1.235e+11 | 3.19615e+11 | |
| ObjA 2 | 17759.5 | 5.68349e+06 | 2.28613e+06 | 7.29661e+08 | 1.92813e+09 | 3.0373e+08 | 6.88084e+11 | 2.47358e+11 | 9.65996e+10 | 4.14146e+10 | |
| ObjB 13 | 16650.5 | 4.5397e+06 | 4.74617e+06 | 1.2621e+09 | 1.27477e+09 | 1.39666e+09 | 3.67914e+11 | 3.45878e+11 | 3.62496e+11 | 4.23443e+11 | |
| ObjB 14 | 8188 | 3.73339e+06 | 1.88459e+06 | 8.60065e+08 | 1.70432e+09 | 4.51198e+08 | 7.78961e+11 | 3.92987e+11 | 2.06124e+11 | 1.11892e+11 | |
| ObjB 11 | 16549 | 1.40598e+06 | 3.5126e+06 | 3.01685e+08 | 1.27815e+08 | 8.17047e+08 | 1.22805e+10 | 2.77511e+10 | 7.10363e+10 | 2.03854e+11 | |
| ObjB 12 | 16554 | 4.89893e+06 | 1.73768e+06 | 5.10946e+08 | 1.52135e+09 | 1.90774e+08 | 4.92481e+11 | 1.57984e+11 | 5.5699e+10 | 2.17828e+10 |
Spatial moments is raw moments. It used for calculation other types of moments
Spatial moments (0,0) is same value as contour area. If you look on the formulla it is just count of pixels
- Spatial moments (0,0) can be used for compare objects which has different area. For example Object A and B has simillar area so (0,0) is not good option. It can be used for detection object 4 or 14, because the have different area
- Spatial moments (1,0) or (2,0) or (3,0) can detect horizontal objects (Object 2 and 12)
- Spatial moments (0,1) or (0,2) or (0,3) can detect verical objects (Object 11 and 1)
- Spatial moments (1,1) can be used for detection differences between Object A and Object B, but it can be wrong results on rotated objects (13 and 3)
Central moments
Central moments are calculated according follow formula:
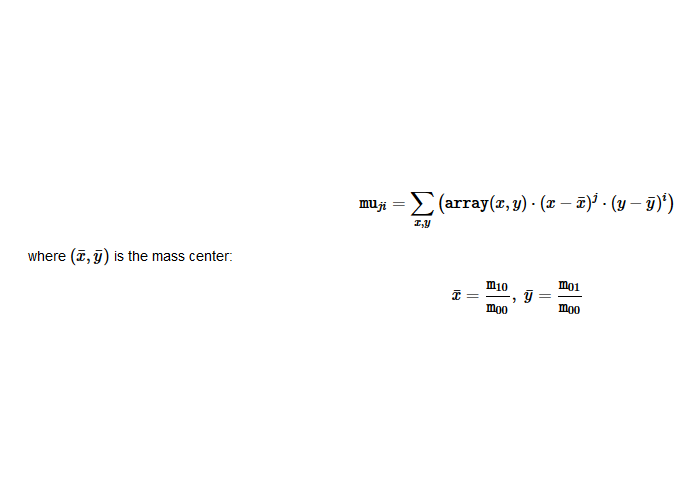
Central moments use the mass center calculated from spatial moments. Central moments (0,0) is same as a spatial moments (0,0), central moments (1,0) (0,1) is zero
Table bellow show central moments on both objects on the picture above.
Table bellow show central moments on both objects on the picture above.
| (2 0) | (1 1) | (0 2) | (3 0) | (2 1) | (1 2) | (0 3) | ||
|---|---|---|---|---|---|---|---|---|
| ObjA 3 | 5.73947e+07 | -4.98137e+07 | 6.11254e+07 | 6.57369e+08 | -5.94336e+08 | 2.32032e+08 | 9.91759e+07 | |
| ObjA 4 | 2.96483e+06 | 605708 | 3.45458e+07 | -2.75378e+07 | 2.28825e+07 | 9.63112e+07 | -2.66864e+08 | |
| ObjA 1 | 9.44212e+06 | 1.95917e+06 | 1.09269e+08 | -1.14698e+08 | 9.73089e+07 | 4.08835e+08 | -1.09688e+09 | |
| ObjA 2 | 1.09269e+08 | -1.95917e+06 | 9.44212e+06 | 1.09688e+09 | 4.08835e+08 | -9.73089e+07 | -1.14698e+08 | |
| ObjB 13 | 3.70346e+07 | -3.19304e+07 | 4.37821e+07 | 1.58183e+08 | -7.96574e+07 | -9.66333e+07 | 3.68412e+08 | |
| ObjB 14 | 2.04315e+06 | 769837 | 1.74324e+07 | -571925 | 1.09706e+07 | 4.17462e+07 | 1.76256e+07 | |
| ObjB 11 | 8.36398e+06 | 3.25848e+06 | 7.14823e+07 | 367750 | 6.82476e+07 | 2.37686e+08 | 8.72112e+07 | |
| ObjB 12 | 7.15813e+07 | -3.29803e+06 | 8.36821e+06 | -1.09078e+08 | 2.38701e+08 | -6.55965e+07 | 227269 |
- Central moments (1 1) on the same moments are equal in horizontal and vertical position.(Object 1 and 2) (Object 11 and 12) but it is not same if is object rotated on some angle(Object 1 and 3)
- Central moments can be used for detect different objects. (Obj A, Obj B) has different values
- If object is same but scaled (Object 1 and 4)(Object 11 and 14) valeus are different, so if object is scaled is detected as different object
Normalized Central moments
Normalized Central moments are calculated according follow formulla:
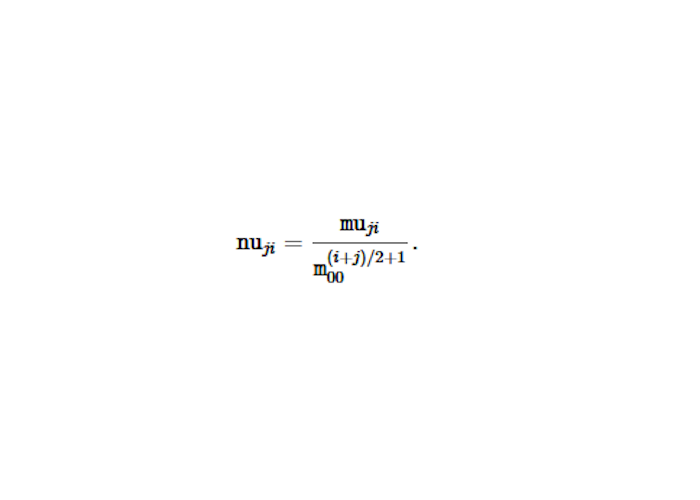
Normalized central moments use central moments which is devided with contour area powered according (i,j) . Normalized Central moments (0,0) is 1, normalized central moments (1,0) (0,1) is zero
Table bellow show central moments on both objects on the picture above.
Table bellow show central moments on both objects on the picture above.
| (2 0) | (1 1) | (0 2) | (3 0) | (2 1) | (1 2) | (0 3) | ||
|---|---|---|---|---|---|---|---|---|
| ObjA 3 | 0.182426 | -0.15833 | 0.194284 | 0.0156884 | -0.0141841 | 0.00553753 | 0.00236687 | |
| ObjA 4 | 0.0300708 | 0.0061434 | 0.350381 | -0.00280292 | 0.00232908 | 0.00980298 | -0.0271626 | |
| ObjA 1 | 0.029937 | 0.00621169 | 0.346444 | -0.00272884 | 0.00231513 | 0.00972683 | -0.0260964 | |
| ObjA 2 | 0.346444 | -0.00621169 | 0.029937 | 0.0260964 | 0.00972683 | -0.00231513 | -0.00272884 | |
| ObjB 13 | 0.133583 | -0.115173 | 0.157922 | 0.00442172 | -0.00222668 | -0.00270121 | 0.0102983 | |
| ObjB 14 | 0.030475 | 0.0114827 | 0.260016 | -9.42746e-05 | 0.00180836 | 0.00688133 | 0.00290535 | |
| ObjB 11 | 0.03054 | 0.0118979 | 0.261009 | 1.04381e-05 | 0.00193713 | 0.00674644 | 0.00247539 | |
| ObjB 12 | 0.261212 | -0.0120351 | 0.030537 | -0.00309371 | 0.00677011 | -0.00186047 | 6.44588e-06 |
- Normalized central moments has same value for same objects but scaled (Object 1 and 4) (Object 11 and 14), so it can be used for detect objects which is scalled
- Normalized central moments has different value for same object but in horizontal or vertical position
- Rotated objects has different value on same objects
HU moments
HU moments are calculated according follow formulla:
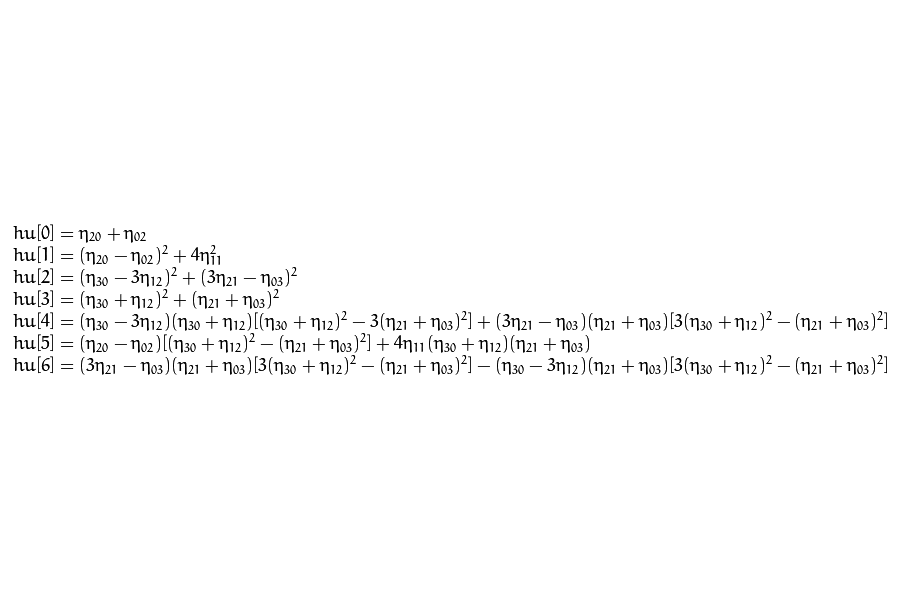
Hu moments are calculated from Normalized central moments. There are 7 HU moments. The first six moments are invariant to the image scale,rotation and reflection.
The seventh one is invariant only to the image scale, rotation. Sign of seventh is changed according reflection.
| HU0 | HU1 | HU2 | HU3 | HU4 | HU5 | HU6 | ||
|---|---|---|---|---|---|---|---|---|
| ObjA 3 | 0.37671 | 0.100415 | 0.00201858 | 0.000590186 | 6.42718e-07 | 0.00015517 | -4.33658e-08 | |
| ObjA 4 | 0.380452 | 0.102749 | 0.00220382 | 0.000665705 | 8.04458e-07 | 0.000177569 | -5.48277e-08 | |
| ObjA 1 | 0.376381 | 0.100331 | 0.00210997 | 0.000614522 | 6.96882e-07 | 0.000159366 | -6.33078e-08 | |
| ObjA 2 | 0.376381 | 0.100331 | 0.00210997 | 0.000614522 | 6.96882e-07 | 0.000159366 | -6.33078e-08 | |
| ObjB 13 | 0.291505 | 0.0536514 | 0.000445148 | 6.8111e-05 | 3.56325e-09 | -4.88411e-06 | 1.13119e-08 | |
| ObjB 14 | 0.290491 | 0.0532166 | 0.000436424 | 6.82831e-05 | 4.27595e-09 | -4.00399e-06 | 1.09847e-08 | |
| ObjB 11 | 0.291549 | 0.0536821 | 0.000420337 | 6.51257e-05 | 3.473e-09 | -4.61593e-06 | 1.02002e-08 | |
| ObjB 12 | 0.291749 | 0.0537905 | 0.000418437 | 7.04657e-05 | 5.20806e-09 | -3.31515e-06 | 1.09217e-08 |
- Normalized central moments has same value for All A objects (same objects with various rotation, scale)
- Value between objects A and objects B are different , so HU moments can be used for separation of different shape of objects
- If your objects change rotation or it is scale , use HU moments
- Hu moments are the most used moments in object detection